Übersicht:

Zustandskurve von Temperatur, Taupunkt und Wind     

Das thermodynamische Diagramm wird von der Karte aus durch Anklicken der darzustellenden Temp-Station geöffnet und zeigt den druckabhängigen Verlauf von Temperatur, Taupunkt und Wind (Zahlengruppen DDD/FFF oder Windfiedern). Alternativ kann das Diagramm auch über die Karten-Menuoption Datei/Temps/Diagramm geöffnet werden, beim ersten Mal erscheint ein leeres Diagramm.

Bis zu drei ausgewählte TEMPs lassen sich gleichzeitig darstellen. Standardmäßig kennzeichnet GELB (bei dunklem Hintergrund, andernfalls BRAUN) den jeweils zur Auswertung aktivierten TEMP. Die anderen TEMPs werden in GRAUtönen im Hintergrund gehalten.

Die zugehörigen Kennungen erscheinen am oberen Ende des Diagramms. Ein Mausklick auf eine Kennung aktiviert den jeweiligen TEMP. Die rechte Maustaste öffnet ein Kontextmenu mit Optionen zur Änderung der Farbcodierung sowie zum Löschen des TEMPs (Löschen geht auch mit Doppelklick).

Es gibt folgende Möglichkeiten, TEMPs nachzuladen:

Datei / Datei öffnen   Strg-D Auswahl einer .TLP-Datei aus dem Dateiverzeichnis. Anschließend erscheint die TEMP-Auswahlliste. Durch Wiederholen dieser Option können auch TEMPs von verschiedenen Dateien gleichzeitig geladen werden. Die folgenden Optionen sind nur sichtbar, wenn mindestens ein TEMP geladen ist. Datei / Temp Auswahl   Strg-T Die Auswahlliste zeigt alle TEMPs einer .TLP-Datei. Datei / Temp Vorgänger   Strg-V Das Dateiverzeichnis wird durchsucht nach bis zu zwei zeitlich nächstgelegenene Vorgängern des aktiven TEMPs der und stellt im Erfolgsfall alle drei neu dar.

Die beiden folgenden Funktionen starten entweder die Auswahlliste (TLOGP-light), oder zeigen wieder die Karte.

Mit der Menuoption Diagramm/Profile oder Klick auf öffnet sich rechts neben dem Diagramm ein zweites Fenster zur Profildarstellung verschiedener, aus den Basisdaten abgeleiteter Parameter.

Datei / Temp sichern   Strg-S
Der jeweils aktive TEMP läßt sich in einer Datei beliebigen Namens speichern (anhängen oder überschreiben).

Vor dem Sichern kann ein mehrzeiliger Kommentar hinzugefügt werden, der in gekürzter Form hinter der Stationskennung erscheint und vollständig als Liste eingeblendet werden kann : (nur sichtbar, wenn Kommentar vorhanden)

TEMP-Auswahlliste     

Der TEMP-Auswahl-Dialog zeigt alle TEMPs einer .TLP-Datei, und zwar entweder nach Terminen (Standard) oder nach Stationen sortiert.

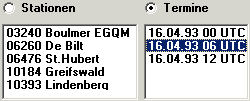	Im ersten Fall zeigt die linke Liste alle Stationen des in der rechten Liste angeklickten Termins. Klicken Sie in der linken Liste, um TEMPs in die Auswahl zu übernehmen.
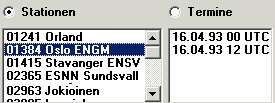	Im zweiten Fall zeigt die rechte Liste alle Termine der in der linken Liste angeklickten Station. Klicken Sie in der rechten Liste, um TEMPs in die Auswahl zu übernehmen.
	Maximal 3 TEMPs können ausgewählt werden. Klicken Sie auf einen ausgewählten TEMP, um ihn aus der Auswahl zu streichen.
	TEMPs, die bereits einmal im Diagram dargestellt waren, werden protokolliert und können zurückgeholt werden.

Diagramm-Einstellungen     

Die graphischen Eigenschaften des thermodynamischen Diagramms werden über das Hauptmenu eingestellt         Diagrammpapier Zur Auswahl stehen das Adiabatenpapier nach Stüve sowie das schiefwinklige T-log-p - Diagramm nach Herlofson. Beide Diagramme zeigen die folgenden Hilfslinien : Isothermen Isobaren Trockenadiabaten Feuchtadiabaten	Adiabaten ein- und ausblenden. Wind Strg-W Darstellung graphisch oder numerisch. Höhenangaben in alpahnumerischen Auswertungen
ICAO-Atmosphäre Strg-I ein- und ausblenden. Am Bildrand befindet sich außerdem die Höhenskala der ICAO-Standardatmosphäre, links in Hektofuss (Flight Level), rechts in km. Ihr Temperaturverlauf läßt sich mit der Menu-Option Diagram/ICAO-Atmosphäre oder mit der Tastenkombination Strg-I einblenden .
Farbe Die Hintergrundfarbe ist beliebig einstellbar. Es ist jedoch entweder Weiss oder Schwarz zu empfehlen, da die Hilfslinienscharen nur zwei verschiedene, an die Hintergrundhelligkeit angepaßte Farben annehmen können.	Schrift Die Beschriftungen der Linien und der TEMP-Kennungen lassen sich nur einheitlich in Größe, Art und Stil einstellen, die Farbe ist vorgegeben.

Diagramm-Funktionen     

Die Funktionen zur Skalierung uns Auswertung des thermodynamischen Diagramms werden über das über die Schalterleiste am rechten Bildrand gesteuert

	Nach rechtem Mausklick öffnet sich ein Pop-Up-Menu, mit dem zusätzliche Hilfslinien gezeichnet werden können, insbesondere Linien des Sättigungsmischungsverhältnisses, die aus Gründen der Übersichtlichkeit nicht von vornherein im Diagramm dargestellt werden.
Außerdem lassen sich mit der Menu-Option Feuchteparameter einige Eigenschaften feuchter Luft an der Cursorposition berechnen. War vor der Menuöffnung die linke Maustaste gleichzeitig gedrückt, so werden Temperatur und Taupunkt der aktuellen Zustandskurve entnommen, andernfalls wird das fehlende Feuchtemaß interaktiv abgefragt.	Im negativen Temperaturbereich muss vor Eingabe eines Feuchtemaßes,wegen der energetisch unterschiedlichen Phasenübergänge fest<->gas und flüssig<->gas, entschieden werden, ob die Luftmasse unterkühltes Wasser oder Eis enthält.

TEMP-Ausdruck     

Der Ausdruck eines Diagramms kann auf den Drucker oder in eine Datei (Bitmap-Format .BMP) erfolgen. Bei gleichzeitiger Darstellung eines Vertikalprofils auf dem Bildschirm werden beide Diagramme analog nebeneinander gedruckt. Nur in diesem Fall kann das Ausgabeformat (hochkant oder quer) gewählt werden. Im Hochkantformat ist ausreichend Platz vorhanden, um die Ergebnisse der zuletzt durchgeführten TEMP-Auswertung unterhalb der Grafik(en) in einer Textbox anzufügen.

Trocken- und Feuchtadiabaten     

Ein Radiosondenaufstieg liefert Temperatur und Feuchte nicht als Funktion der Höhe sondern des Luftdruckes. Aber nicht nur deshalb wird der Druck als die Ordinate in Diagrammpapieren benutzt.

Die vertikale Temperatur- und Feuchteschichtung bestimmen die Dichteschichtung in der Atmosphäre. Die Stabilität der Schichtung steuert den Ablauf von Vertikalbewegungen. Schichten unterschiedlicher Schichtungsstabilität können übereinander angeordnet sein.

Die Schichtung in einem bestimmten Höhenintervall wird als stabil angenommen, wenn ein vertikal angestossenes Luftpaket wieder in seine Ausgangsposition zurückkehrt. Labilität ist dagegen gegeben, wenn vertikale Umlagerungen zustande kommen.

Trockendiabaten
Zur Analyse aktueller Stabilitätsverhältnisse verwendet man die vereinfachte Vorstellung, daß während der relativ schnell ablaufenden Bewegungen diabatische Prozesse, also Strahlung und fühlbare Wärmeflüsse, vernachlässigbar sind. Dieses Modell der adiabatischen Zustandsänderungen verknüpft Druck und Temperatur auf eindeutige Weise und läßt sich daher in einem Diagramm mit Druckordinate als Kurvenschar, die (Trocken-) Adiabaten, darstellen.

Adiabaten sind Linien konstanter potentieller Temperatur und beschreiben die Temperaturänderung auf- und absteigender Luftpakete, wenn kein Wärmeaustausch mit der umgebenden Luft zugelassen wird. Die potentielle Temperatur ist die Temperatur, die ein Teilchen annimmt, wenn es adiabatisch auf den Normaldruck 1000 hPa gebracht wird. Der trockenadiabatische Temperaturgradient beträgt -1K/100m.

In ein Diagramm mit metrischer Ordinate lassen sich dagegen keine Adiabaten drucken, denn deren Verlauf hinge von den aktuellen Messwerten ab. Die dennoch in Diagrammen angegebenen metrischen Skalenwerte beziehen sich auf die ICAO-Standardatmosphäre und gelten nicht exakt für den aktuellen Aufstieg.

Aus der Neigung des aktuellen Zustandskurve gegenüber der zugehörigen Adiabaten kann somit auf die Dichteunterschiede zwischen angestossenem Luftpaket und Umgebungsluft geschlossen werden.

Bei trocken-stabiler Schichtung nimmt die Temperatur in der Atmosphärenschicht mit der Höhe um weniger als 1 Grad/100 ab, die Temperaturabnahme ist geringer als der trocken-adiabatische Temperaturgradient. Luftteilchen, die gehoben werden, kühlen sich rascher als die Umgebungsluft ab und werden somit kälter und schwerer als ihre Umgebung. Damit sinken sie auf die Höhe ab, in der eine ihrer Dichte entsprechende Temperatur herrscht. Isothermien und Inversionen zählen zu dieser Art der Schichtung.

Ist die Schichtung trocken-labil, so wird das Luftpaket entlang der Adiabaten weiter aufsteigen, bis es wieder stabile Verhältnisse antrifft. Da trocken-labile Schichtungen sofort vertikale Umlagerungen auslösen, werden sie nur in Bodennähe, verursacht durch Sonneneinstrahlung, angetroffen.

In Gegenwart von Wasserdampf muß das trockenadiabatische Modell erweitert werden. Der Wasserdampfgehalt der Atmospäre wird z.B. beschrieben durch das Mischungsverhältnis, das ist das Verhältnis der Wasserdampfdichte zur Dichte trockener Luft.

Da der maximale Wasserdampfgehalt d.h. der Sättigunsdampfdruck eines Luftvolumens nur von seiner Temperatur abhängt, lassen sich die Linien konstanten Sättigungsmischungsverhältnisses ebenfalls als Kurvenschar darstellen. Unter der vereinfachenden Annahme, das sich der absolute Wasserdampfgehalt in einem aufsteigenden Luftpaket nicht ändert, dienen diese Linien zusammen mit den Adiabaten der Ermittlung des Kondensationsniveaus bei Hebung.

Feuchtadiabaten
Wird ein Luftpaket über das Kondensationsniveau hinaus gehoben, wird die adiabatische Temperaturabnahme durch das Freiwerden von Kondensationswärme gemindert. Diese Temperaturänderung austeigender Luftpakete mit gesättigtem Wasserdampf ist wiederum nur eine Funktion des Luftdruckes und wird durch eine weitere Kurvenschar, die Feuchtadiabaten beschrieben. Ihre Temperaturabnahme beträgt je nach Höhe 0.4 bis 1 Grad/100, sie hängt von der absoluten Feuchte der Luftmasse ab. In großen Höhen mit geringer absoluter Feuchte nähern sich die Feuchtadiabaten deshalb den Trockenadiabaten an.

Ein in feuchtlabiler Schichtung angehobenes feuchtgesättigtes Luftpaket kühlt also gegenüber der umgebenden wolkenfreien Luft weniger stark ab und sein Auftrieb wird beschleunigt.

Bei einem vollständigen feuchtadiabatischen Prozeß wird ein Luftquantum entlang der Feuchtadiabaten zu niedrigen Drücken und Temperaturen geführt, bis der Wasserdampf vollständig ausgefallen ist. Der weitere Weg wird entlang der Trockenadiabate verfolgt, der sich asymptotisch genähert wurde, bis wieder 1000 hPa Druck erreicht worden sind. Die jetzt angenommene Temperatur heißt pseudopotentielle Temperatur. Die Feuchtadiabaten werden daher als Linien konstanter pseudopotentielle Temperatur auch als Pseudoadiabaten bezeichnet.

Der Föhn-Prozess Der Föhn ist ein trockener Fallwind im Lee von Gebirgszügen. Er entsteht beim Überströmen hoher Gebirge und erhält seine typischen Eigenschaften (Wolkenauflösung, Trockenheit, Wärme) dadurch, daß sich die im Luv aufsteigende nach Erreichen des Kondensationsniveaus (Wolkenbildung) nur noch um 0.65 C/100 m abkühlt, aber nach Überströmen des Gebirgskammes unter Wolkenauflösung um 1 C/100 m erwärmt.

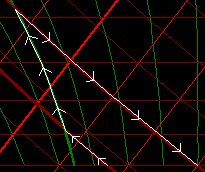Die Luft kommt also auf der Leeseite auf gleicher Höhe viel wärmer an. Besonders heftig weht der Föhn durch enge Täler, wobei in Böen auch Orkanstärke erreicht werden kann. Der Name kommt aus dem lateinischen favonius=(milder) Westwind und wurde auf den (milden bzw. warmen) Föhn im Alpenraum übertragen, wenngleich dieser entweder aus Nord oder Süd weht.

Das Stüve-Diagramm     

Das thermodynamische Diagramm nach Stüve (1922, neuberechnet von Hinkelmann, 1950) wird vom Deutschen Wetterdienst benutzt und findet ebenso in Mitteleuropa häufige Anwendung. Es hat T [C] als Abszisse mit den Isothermen als senkrechte Geraden und p als Ordinate mit waagerechten Isobaren.

Die von rechts unten nach links oben gerade verlaufenden Trockenadiabaten schneiden sich im außerhalb des Diagramms liegenden Nullpunkt von Luftdruck und Temperatur. Die Feuchtadiabaten verlaufen mit einer Linkskrümmung von rechts unten nach links oben und nähern sich dabei asymptotisch den Trockenadiabaten. Die Linien gleichen Sättigungsmischungsverhältnisses verlaufen fast senkrecht von rechts unten nach links oben.

Das Stüve-Diagramm enthält zusätzlich Angaben zur Berechnung der absoluten Höhen der ICAO-Standardatmosphäre. Die Vorteile des Stüve-Diagramms liegen zum einen in der Geradlinigkeit der drei Linienscharen t=const, p=const und (Theta)=const Zum anderen ist es wegen der (p hoch k)-Koordinate auch für hochreichende Aufstiege handlich, weil sie die niedrigen Drücke zusammendrängt.

Nachteilig ist, daß mit Hilfe dieses Diagramms unmittelbar keine thermodynamischen Arbeitsleistungen, also atmosphärische Energieänderungen, bestimmt werden können. Für exakte Energiebetrachtungen müssen seine Flächen mit einem Faktor korrigiert werden, da sie keine flächentreue Abbildung des p,V-Diagramms geben. Jedoch ist der Fehler in der Flächenbestimmung wiederum im allgemeinen so klein, daß er für praktische Zwecke meist vernachlässigbar ist.

Flächentreue wurde erst mit der Konstruktion des Emagramms (Energie pro Masseneinheit, Refsdal, 1932) erreicht. Die Koordinaten sind T in linearer Skala als Abszisse und der Logarithmus des Luftdrucks, log p, als Ordinate. Das Diagramm ähnelt dem Stüve-Diagramm sehr, nur sind hier die Trockenadiabaten keine Geraden.

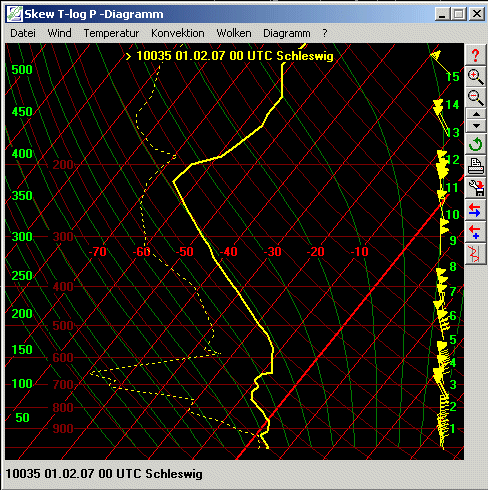
Das T-logP-Diagramm nach Herlofson     

Das insbesondere im US- und teilweise im deutschen Flugwetterdienst verwendete SkewT-logP-Diagramm (Herlofson, 1947) wird auch vom Geophysikalischen Beratungsdienst der Bundeswehr benutzt. Es entspricht dem Emagramm , wobei aber die Linien p=const. und T=const. nicht senkrecht aufeinander stehen, sondern sich unter einem Winkel von 45 Grad schneiden. Dabei verlaufen die Isobaren in logarithmischen Abständen waagerecht und die Isothermen in äquidistanten Abständen schräg von links unten nach rechts oben (SkewT = schiefes T).

Die Adiabaten sind unter leicht konvexer Krümmung von rechts unten nach links oben gerichtet. Die Feuchtadiabaten, ebenfalls von rechts unten nach links oben verlaufend, nähern sich mit abnehmendem Druck und abnehmender Temperatur asymptotisch den Trockenadiabaten.

Neben diesen Linien enthält das Diagramm ebenfalls Linien gleichen Sättigungsmischungsverhältnisses, die in einem Winkel von etwa 60 Grad zu den Isobaren von links unten nach rechts oben verlaufen. Außerdem existieren Linien für die Kondensstreifenvorhersage sowie den Temperaturverlauf der ICAO-Standardatmosphäre.

Vorteilhaft ist die Flächentreue für Energiebetrachtungen in allen Luftdruckniveaus. Durch die Schiefwinkligkeit des Koordinatensystems schneiden sich die Isothermen und die Adiabaten fast unter dem für Flächenbestimmungen idealen Winkel von 90 Grad.

Auch die Trocken- und Feuchtadiabaten treffen sich unter relativ großen Winkeln, was die Betrachtung der Stabilitätsverhältnisse erleichtert. Die logarithmische Druckskala hat den Vorteil, daß die Druck-Höhen-Kurve nahezu eine Gerade ist. Durch diese Anordnung der Linienscharen treten bei eingetragenen Zustandskurven große Temperaturgefälle (deutlich nach links gekippt), Isothermien und Inversionen (auffällig nach rechts gekippt) sehr gut hervor.

Nachteilig wirkt sich aus, daß bei der Darstellung hochreichender Aufstiege die Druckskala bei niedrigen Drücken sehr auseinandergezogen ist. Dadurch beanspruchen die energetisch weniger interessanten Höhenschichten viel Platz.

Geopotential     

Wird eine Masseneinheit vom Meeresniveau auf eine bestimmte Höhe gehoben, muss Arbeit zur Überwindung der Schwerkraft geleistet werden. Die Schwerebeschleunigung g ist aber eine, nicht nur von der Höhe z, sondern auch von der geographischen Breite φ abhängige Größe. Ursache dafür ist die Drehung und Abplattung der Erde. Die Zentrifugalbeschleunigung der Erddrehung wirkt der Gravitation entgegen - sie ist am Äquator maximal und verschwindet an den Polen. Demnach ist Arbeitsleistung erforderlich, um Luftmassen in meridionaler Richtung zu verschieben. Aus diesem Grund wird in der Meteorologie nicht die metrische Höhe z sondern das sogenannte Geopotential h als vertikale Koordinate verwendet.

g(φ,z) dz = g_n dh

Durch die Normierung mit der Konstanten g_n=9.8ms^-2 besitzt das Geopotential h die gleiche Größenordnung wie die metrische Höhe. Flächen gleichen Potentials heißen Geopotentialflächen - ihr Wert wird in geopotentiellen Metern oder Dekametern (gpm, gpdm) angegeben. Die Erdoberfläche (d.h. die ruhende Meeresoberfläche) ist eine Geopotentialfläche mit dem Wert h=0 und wird als Normalnull (NN) bezeichnet.

Barometrische Höhenmessung     

Aufgrund der Kompressibilität der Luft ist der Luftdruck am Erboden am höchsten und nimmt mit der Höhe logarithmisch ab. Die Abnahme beträgt etwa 50% je 5,5 km. In kalter Luft ist die Luftdruckabnahme größer als in warmer Luft. Mit Messung eines Vertikalprofils von Luftdruck, Temperatur und Feuchte kann man mit Hilfe der barometrischen Höhenformel eine Höhenbestimmung durchführen. Der geopotentielle Abstand zweier Druckflächen p und p_oist demnach näherungsweise gegeben als

h - h_o = -R_L T_vm (ln p - ln p_o) / g_n

Als barometrische Höhenstufe bezeichnet man die Höhendifferenz, die einer Luftdruckabnahme von einem Hektopascal entspricht. Bei mittleren Temperaturen beträgt diese Höhenstufe am Erdboden 8 m, in 5,5 km Höhe bei nur noch halbem Luftdruck 16 m. In mittleren Breiten kann diese Stufe in Meereshöhe im Sommer bis zu 10 Prozent höher, im Winter bis zu 10 Prozent niedriger liegen.

Die ICAO-Standardatmosphäre     

Von der ICAO vereinbarte Normalatmosphäre mit allgemein angenommenen Werten einer mittleren, trockenen Atmosphäre konstanter Zusammensetzung, die vor allem für Zwecke der Luftfahrt und für die Eichung von Meßgeräten wie folgt festgelegt worden sind: Luftdruck auf Meeresniveau  1013.25 hPa  Temperatur auf Meeresnveau  15.0°C  Vertikaler Temperaturgradient <11 km  -0.65 K/100m  Vertikaler Temperaturgradient >20 km  -0.1 K/100m  Aus der Standardatmospäre ergibt sich nach der barometrischen Höhenformel eine Höhenskala, die auch ein Maßstab der thermodynamischen Diagramme ist. In der Luftfahrt werden barometrische Höhenmesser benutzt, die sich auf die Standardatmosphäre beziehen. Die Druckhöhen der Standardatmosphäre in der Einheit 'hektofeet' werden als Flugflächen (Flightlevel FL) bezeichnet.

p/hPa  h/gpm  h/ft  T/°C  1013.25  0  0  15.0  1000  111  334  14.3  950  540  1.772  11.5  850  1.457  4.780  5.5  700  1.949  6.394  -4.6  600  4.206  13.799  -12.3  500  5.574  18.287  -21.2  400  7.185  23.573  -31.7  300  9.164  30.066  -44.6  250  10.383  34.065  -52.5  200  11.784  38.661  -56.5  150  13.608  44.646  -56.5  100  16.180  53.084  -56.5

Höhenmessung in der Luftfahrt     

Die barometrische Höhenmessung ist noch immer die einzige Möglichkeit der absoluten Höhenmessung. Um vergleichbare Anzeigen zu erhalten, wird ein gemäß der ICAO-Standard-Atmosphäre geeichtes Aneroid-Barometer benutzt. Mit einer Nebenskala kann der Nullpunkt der Höhenmessung auf einen bestimmten Druck eingestellt werden. Die drei folgenden Verfahren sind in Gebrauch:

Das QFE-Verfahren wird wegen der Verfügbarkeit von Radarhöhenmessern bei IFR-Flügen nur noch selten benutzt. Der Höhenmesser wird auf den Luftdruck am Landebahnbezugspunkt (höchster Punkt der Landbahn) eingestellt. Die angezeigte Höhe ist Null bei Landung des Flugzeugs.

Das QNH-Verfahren wird bei VFR-Flügen im unteren Luftraum (5000 ft msl bzw. 200 ft agl, höherer Wert maßgeblich) angewendet. QNH ist der nach der Standardatmospäre reduzierte Luftdruck am Landebahnbezugspunkt. Der Höhenmesser wird nach dem Start vom lokalen QNH auf ein regionales QNH und vor der Landung auf das QNH des Zielplatzes eingestellt. Er zeigt bei Landung die genaue Höhe der Landebahn bezogen auf NN.

Beim QNE-Verfahren wird der Höhenmesser auf 1013.2 hPa eingestellt.Er zeigt bei Landung die Höhe der Landebahn nach der Standardatmosphäre. Im früheren Morse-Funkverkehr hatten die Kürzel QFE,QNH und QNE die Bedeutung einer Anfrage des Piloten an den Tower. QNE ist im Gegensatz zu den Luftdruckwerten QFE und QNH eine Höhenangabe - sie wird auch als Druckhöhe (Pressure Altitude, PA) bezeichnet.

Das Flight-Level-System
wird bei Flügen oberhalb der transition altitude verwendet. Da bei allen Verfahren die Ablesung des Höhenmessers nur am Boden mit den wirklichen Werten übereinstimmt, erfolgt die vertikale Staffelung des Luftverkehrs nicht nach absoluten Höhen, sondern nach Druckfächen. Mit einer Nulleinstellung des Höhenmessers von 1013,25 hPa (einheitlich für alle Flugzeuge) wird auf Flächen konstanten Luftdruckes (Flugflächen) geflogen.

Die Druckunterschiede der Flugflächen sind so gewählt, daß ihnen eine Höhenstufung von 500 oder 1000 ft entspricht. Die Höhe der Flugflächen wird in Hektofuß (hft) angegeben. FL 180 bedeutet eine Höhe von 18.000 ft nach Standardatmosphäre über dem Niveau, in dem ein Luftdruck von 1013.25 hPa herrscht.

Da bei niedrigem Bodenluftdruck die am Boden angezeigte Höhe negativ ist, gewährleistet das Flight-Level-System im unteren Luftraum keine terrain clearance; aus diesem Grunde wird unterhalb des transition levels die Flughöhe auf das lokale QNH bezogen.

Neben der Druckhöhe des Flight-Level-Systems ist die sogenannte Dichtehöhe (Density Altitude, DA) vor allem bei Starts von hochgelegenen und heißen Plätzen (hot-and-high) von Bedeutung. Sie gibt die Höhe in der ICAO-Atmosphäre an, in der dieselbe Dichte herrscht, wie bei den aktuellen Werten von Druck und Temperatur. Nach der Gasgleichung (Zustandsgleichung für ein ideales Gas) ist die Luftdichte bei gleichem Druck umgekehrt proportional zur Temperatur. Positive Temperaturabweichungen bezüglich der ICAO-Atmosphäre (ISA) führen demanch zu einer signifikanten Erhöhung der Dichtehöhe.